画像 何通り 求め方 中学 236609-何通り 求め方 中学受��

順列と組み合わせの公式とその違い 問題付き 理系ラボ

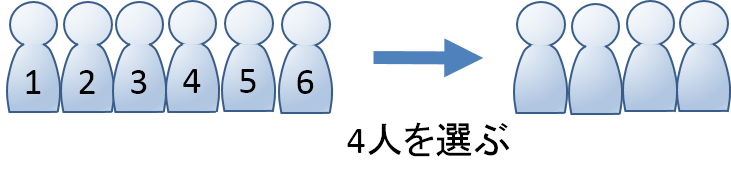
 中学数学の場合の数を求める問題の解き方をわかりやすく教えてほしい このページでは、 「場合の数」について丁寧な解説 を行っていきます。 場合の数は、中学数学の確率の単元 順列の公式 異なる 個のものの中から異なる 個を取り出して 列に並べる場合の数は 補足 ある数から までの整数の積のことを「階乗」といい、記号「 」で表現します。 の階乗 は

何通り 求め方 中学受験

何通り 求め方 中学受験- まとめと公式化 というわけで「12＝ 2① × 2② × 3① と因数分解できるので、12の約数の個数は ( ② 1)× ( ① 1)=3×2=6 と求めることができると分かりました。 12は「2」と「3」のこのように「漸化式を利用して次々に途中までの解を記録していき最終的に解を求める方法」を計算機科学の専門用語で 動的計画法 と言います。 動的計画法の（大学入試に出そうな）他の応用とし

数学 中2 79 確率チャレンジ Lv 1 基本編 Youtube

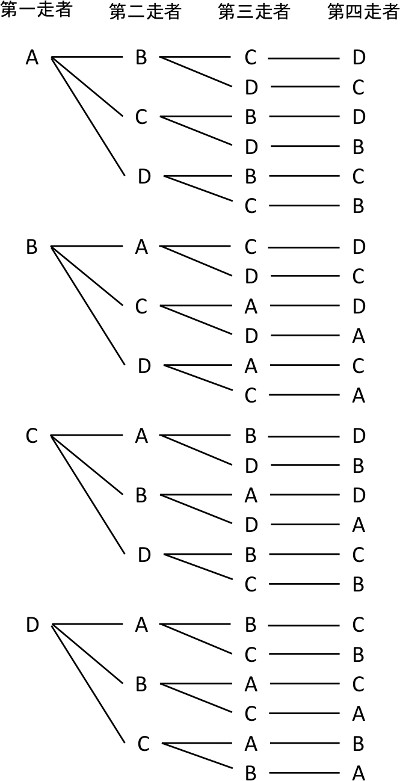
中学入試に出る「組み合わせ」問題パターンと解き方 中学入試で出題される「 場合の数 」の問題には、「 組合せ 」を求めるものと、「 並べ方 」を求める問題があります。 まずは、この2つの違家から学校までの通学路が何通りあるかを求めよう まずは途中に病院があって, 家から病院までの道が \(\color{royalblue}{2}\) 通り, 病院から学校までの道が \(\color{magenta}{3}\) 通り ある場合, 通 それらを全て足すと通りになります。 しかし、赤青と青赤のように同じ組み合わせがあるので、2で割って10です。 数学的に書きますと、5c2 = 10 となります。 今回は小学5~6年

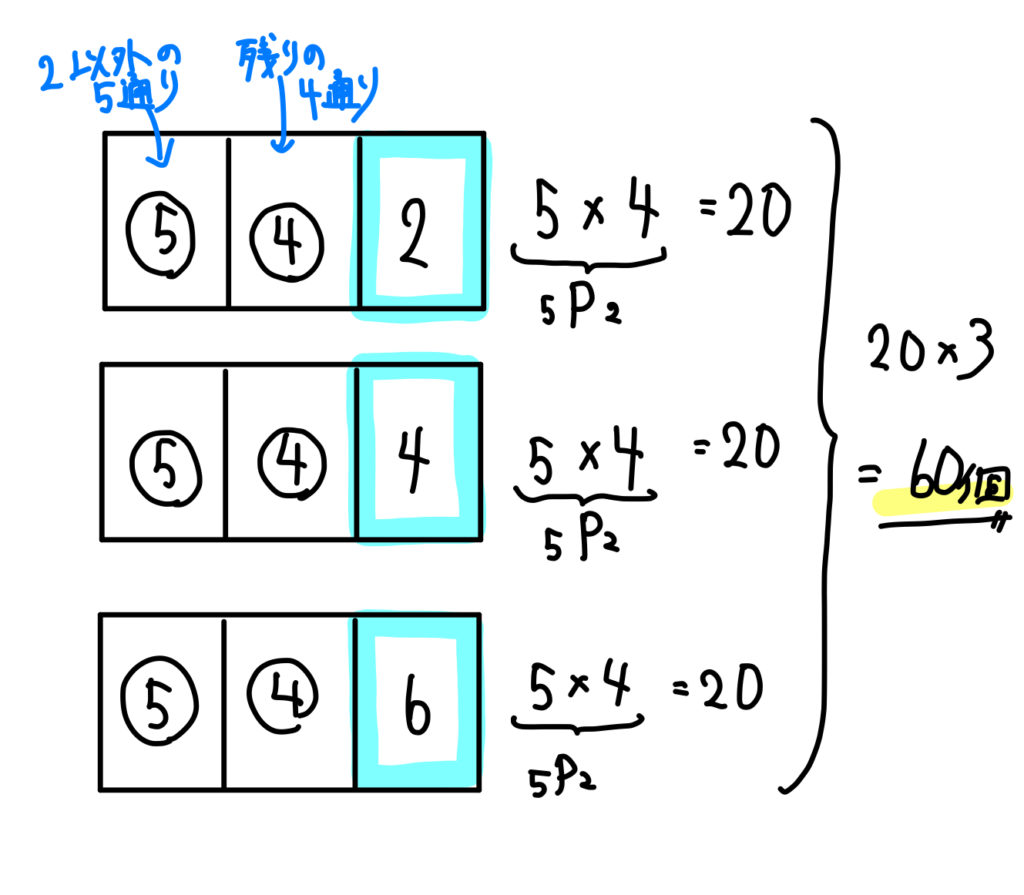
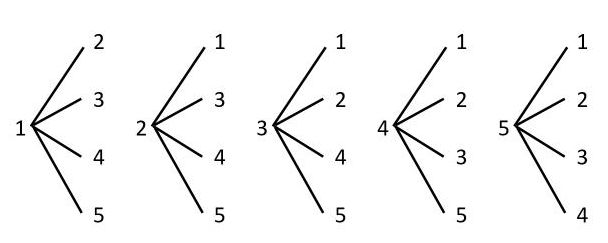
 ②はまず全ての場合の数を計算しましょう。5枚と4枚で連続してカードを引くので5 ️4=通りあります。 そして、連続して奇数となるのは、(1,3), (1,5),(3,1),(3,5),(5,1),(5,3)の6通

何通り 求め方 中学受験のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

2	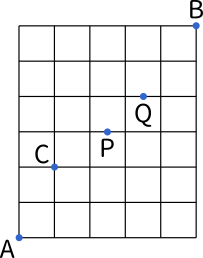2	2
2	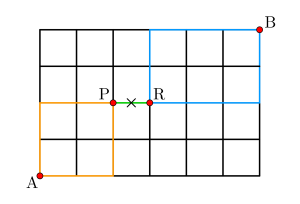2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	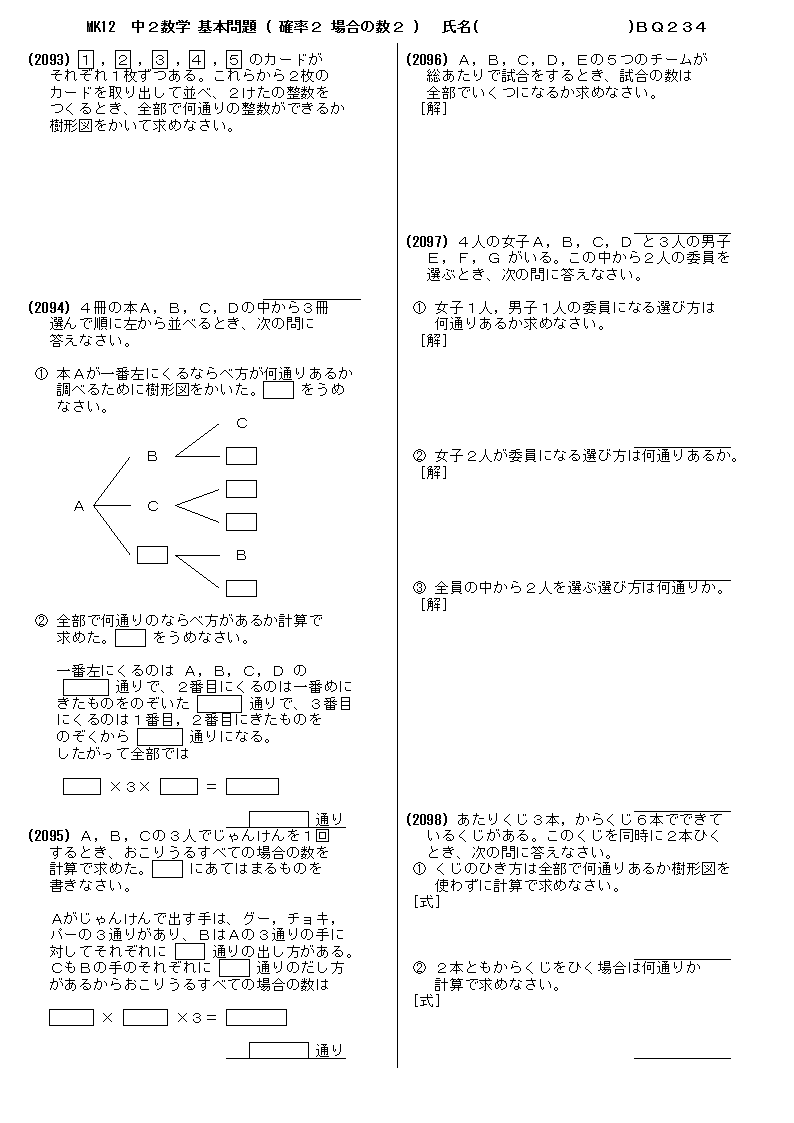2	2
2	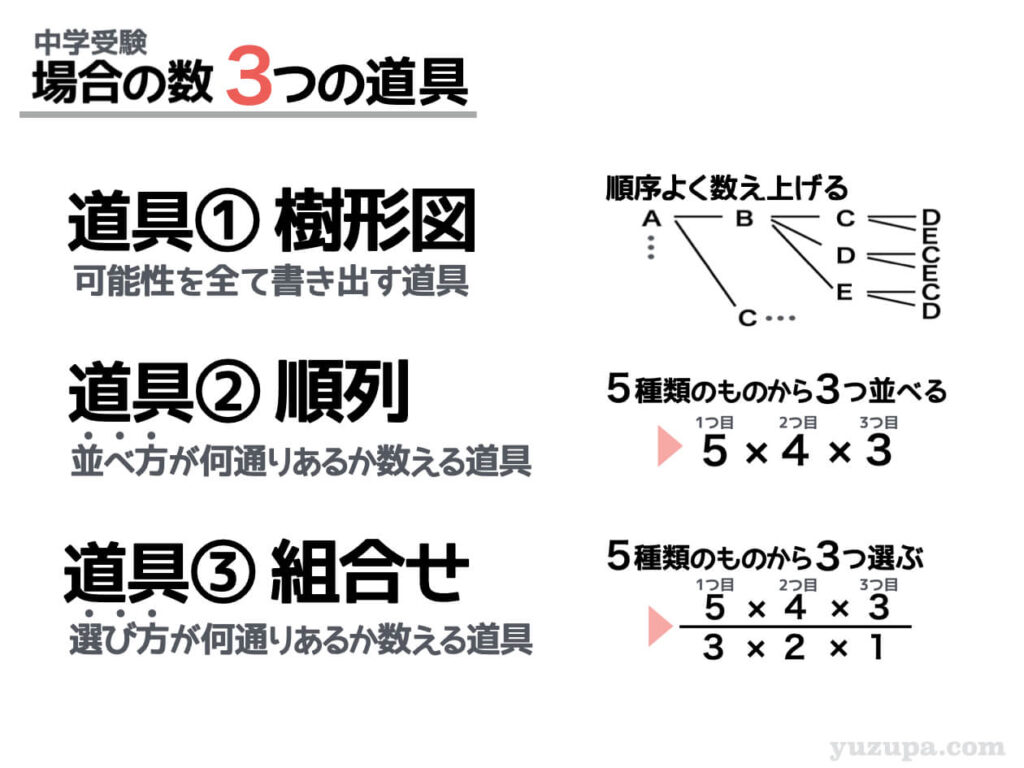2	2
2	2	2
2	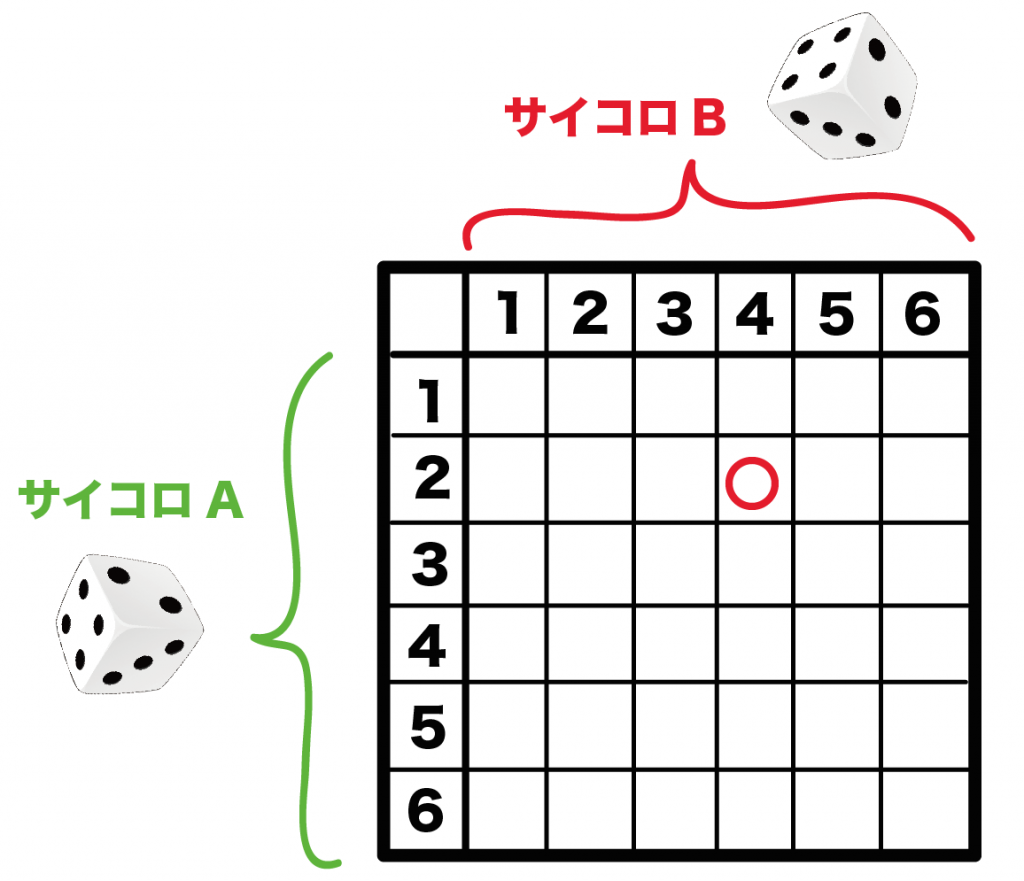2	2
2	2	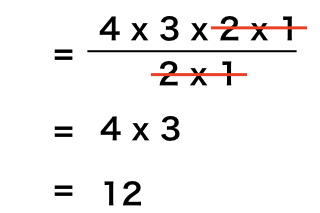2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	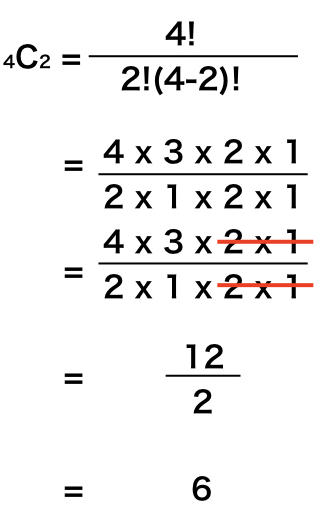2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	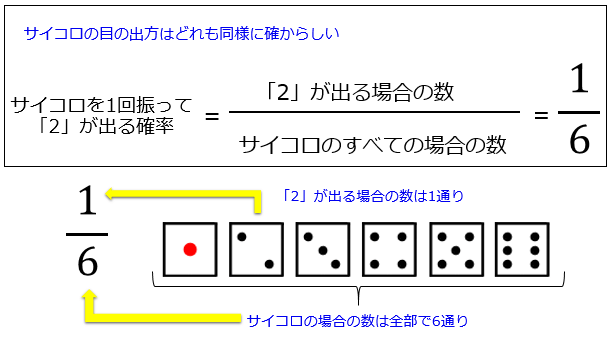2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2	2
2	2

Incoming Term: 何通り 求め方 中学受験, 何通り 求め方 中学,